افزودن لایه ها

شبکه عصبی که ما ساخته ایم قابل احترام تر می شود، اما در حال حاضر، ما فقط یک لایه داریم. شبکه های عصبی زمانی "عمیق" می شوند که 2 یا چند لایه پنهان داشته باشند. در حال حاضر، ما فقط یک لایه داریم که در واقع یک لایه خروجی است. اینکه چرا ما دو یا چند لایه پنهان می خواهیم در فصل بعدی آشکار خواهد شد. در حال حاضر، ما هیچ لایه پنهانی نداریم. لایه پنهان یک لایه ورودی یا خروجی نیست. به عنوان دانشمند، داده ها را همانطور که به لایه ورودی تحویل داده می شوند و داده های حاصل از لایه خروجی را می بینید. لایه های بین این نقاط پایانی دارای مقادیری هستند که ما لزوما با آنها سر و کار نداریم، از این رو نام "پنهان" نامیده می شود. اجازه ندهید این نام شما را متقاعد کند که نمی توانید به این مقادیر دسترسی داشته باشید. شما اغلب از آنها برای تشخیص مسائل یا بهبود شبکه عصبی خود استفاده خواهید کرد. برای بررسی این مفهوم، بیایید یک لایه دیگر به این شبکه عصبی اضافه کنیم، و در حال حاضر، بیایید فرض کنیم که این دو لایه که قرار است داشته باشیم، لایه های پنهان خواهند بود، و ما هنوز لایه خروجی خود را کدگذاری نکرده ایم.

قبل از اینکه لایه دیگری اضافه کنیم، بیایید به این فکر کنیم که چه چیزی در راه خواهد بود. در مورد لایه اول، می بینیم که یک ورودی با 4 ویژگی داریم.

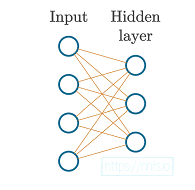
شکل 3.01: لایه ورودی با 4 ویژگی در یک لایه پنهان با 3 نورون.

نمونه ها (داده های مجموعه ویژگی) از طریق ورودی که به هیچ وجه آن را تغییر نمی دهد، به اولین لایه پنهان ما تغذیه می شوند، که می توانیم ببینیم دارای 3 مجموعه وزن است که هر کدام 4 مقدار دارند.
هر یک از این 3 مجموعه وزن منحصر به فرد با نورون متمایز آن مرتبط. بنابراین ، از آنجا که ما 3 مجموعه وزن داریم ، در این اولین لایه پنهان 3 نورون داریم. هر نورون دارای مجموعه ای منحصر به فرد از وزن ها است که 4 مورد از آنها داریم (زیرا 4 ورودی برای این لایه وجود دارد) ، به همین دلیل وزن های اولیه ما شکل (3,4) دارند.
اکنون، می خواهیم یک لایه دیگر اضافه کنیم. برای انجام این کار، باید مطمئن شویم که ورودی مورد انتظار به آن لایه با خروجی لایه قبلی مطابقت دارد. ما تعداد نورون ها را در یک لایه با تعیین تعداد مجموعه های وزن و تعصبات خود تنظیم کرده ایم. تأثیر لایه قبلی بر مجموعه های وزن برای لایه فعلی این است که هر مجموعه وزن باید یک وزن جداگانه برای هر ورودی داشته باشد. این به معنای وزن متمایز در هر نورون از لایه قبلی است (یا اگر در مورد ورودی صحبت می کنیم). لایه قبلی دارای 3 مجموعه وزن و 3 بایاس است، بنابراین می دانیم که دارای 3 نورون است. این بدان معناست که برای لایه بعدی ، ما می توانیم هر تعداد مجموعه وزنی را که می خواهیم داشته باشیم (زیرا این تعداد نورون است که این لایه جدید خواهد داشت) ، اما هر یک از این مجموعه های وزن باید دارای 3 وزن گسسته باشند.
برای ایجاد این لایه جدید، می خواهیم وزن ها و بایاس های خود را در weights2 و biases2 کپی و پیست کنیم و مقادیر آن ها را به مجموعه های ساخته شده جدید تغییر دهیم. در اینجا یک مثال آورده شده است:

inputs = [[1, 2, 3, 2.5],
[2., 5., -1., 2],
[-1.5, 2.7, 3.3, -0.8]]
weights = [[0.2, 0.8, -0.5, 1],
[0.5, -0.91, 0.26, -0.5],
[-0.26, -0.27, 0.17, 0.87]]
biases = [2, 3, 0.5]
weights2 = [[0.1, -0.14, 0.5],
[-0.5, 0.12, -0.33],
[-0.44, 0.73, -0.13]]
biases2 = [-1, 2, -0.5]

در مرحله بعد، اکنون خروجی ها را فراخوانی می کنیم “layer1_ouputs”:

layer1_outputs = np.dot(inputs, np.array(weights).T) + biases

همانطور که قبلا گفته شد، ورودی های لایه ها یا ورودی هایی از مجموعه داده واقعی هستند که با آن آموزش می دهید یا خروجی هایی از لایه قبلی. به همین دلیل است که ما 2 نسخه از وزن ها و بایاس ها را تعریف کردیم اما فقط 1 ورودی - زیرا ورودی های لایه 2 خروجی های لایه قبلی خواهند بود:

layer2_outputs = np.dot(layer1_outputs, np.array(weights2).T) + \
biases2

اکنون همه با هم:

import numpy as np

inputs = [[1, 2, 3, 2.5], [2., 5., -1., 2], [-1.5, 2.7, 3.3, -0.8]]
weights = [[0.2, 0.8, -0.5, 1],
[0.5, -0.91, 0.26, -0.5],
[-0.26, -0.27, 0.17, 0.87]]
biases = [2, 3, 0.5]
weights2 = [[0.1, -0.14, 0.5],
[-0.5, 0.12, -0.33],
[-0.44, 0.73, -0.13]]
biases2 = [-1, 2, -0.5]

layer1_outputs = np.dot(inputs, np.array(weights).T) + biases
layer2_outputs = np.dot(layer1_outputs, np.array(weights2).T) + biases2

print(layer2_outputs)

>
array([[ 0.5031 -1.04185 -2.03875],
[ 0.2434 -2.7332 -5.7633 ],
[-0.99314 1.41254 -0.35655]])

در این مرحله، شبکه عصبی ما می تواند به صورت بصری به صورت زیر نشان داده شود:

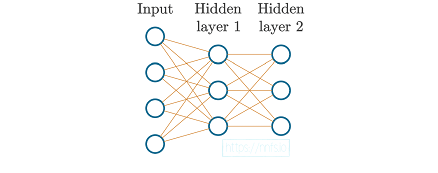
شکل 3.02: 4 ویژگی ورودی به 2 لایه پنهان از 3 نورون است.

داده های آموزشی

در مرحله بعد، به جای تایپ دستی در داده های تصادفی، از تابعی استفاده می کنیم که می تواند داده های غیر خطی ایجاد کند. منظور ما از غیر خطی چیست؟ داده های خطی را می توان با یک خط مستقیم متناسب یا با آن نشان داد.

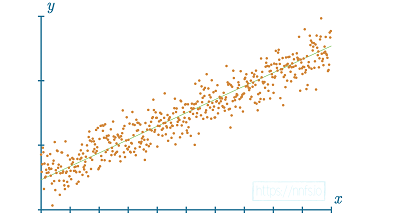
شکل 3.03: نمونه ای از داده ها (نقاط نارنجی) که می توانند با یک خط مستقیم (خط سبز) نشان داده شوند (مناسب).

داده های غیر خطی را نمی توان با یک خط مستقیم به خوبی نشان داد.

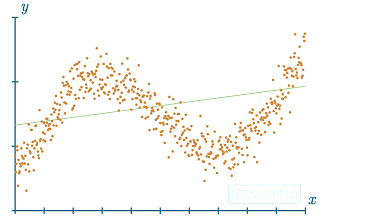
شکل 3.04: نمونه ای از داده ها (نقاط نارنجی) که به خوبی با یک خط مستقیم متناسب نیستند.